Shear-flow Separation of Enantiomers

By Anderson D. S. Duraes

This is an interdisciplinary project touching on Chemistry, Physics, Mathematics, Computer Science and Engineering.

This work appears in J. Phys. Chem. B 2021, 125, 42, 11709–11716. 10.1021/acs.jpcb.1c07127
and also on ChemRxiv: 10.26434/chemrxiv-2021-196zw

Chemistry

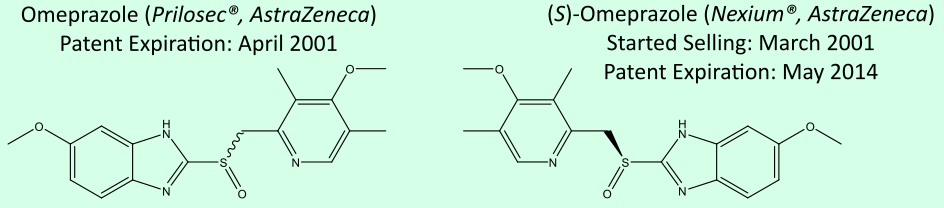
Enantiomers (or chiral molecules) are two compounds with the same structural formula, but which are non-superimposable mirror images. Due to their identical physical and chemical properties in an achiral environments such as water, the separation (or resolution) of the enantiomers is expensive and involves either chiral columns or the use of diasteromers during synthesis.

**Figure 1**: Prilosec^® is a 1:1 (racemic) mixture of the *(R)* and *(S)*–Omeprazole enantiomers. Enantiomeric separation is expensive, but a pure enantiomer can receive a separate patent like Nexium^® (the isolated *(S)*-Omeprazole enantiomer).

Physics

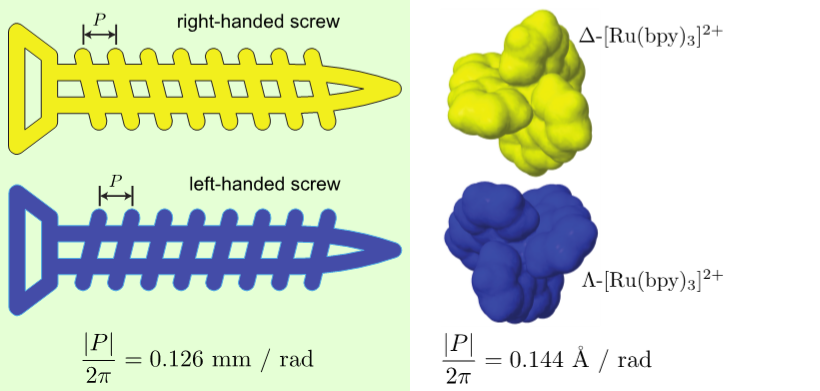
Left- and right-handed screws are also chiral objects that couple rotation around one axis with displacement along that axis. The displacement (in opposite directions) can be measured with a geometric property of the screw: its pitch. In a lab-fixed frame, left- and right-handed screws have pitches with the same magnitude, but with flipped signs, rotating in opposite directions to do the same task.

Under the same counterclockwise rotation, the video shows that the blue (left-handed) screw moves down and the yellow (right-handed) screw moves up.

Mathematics

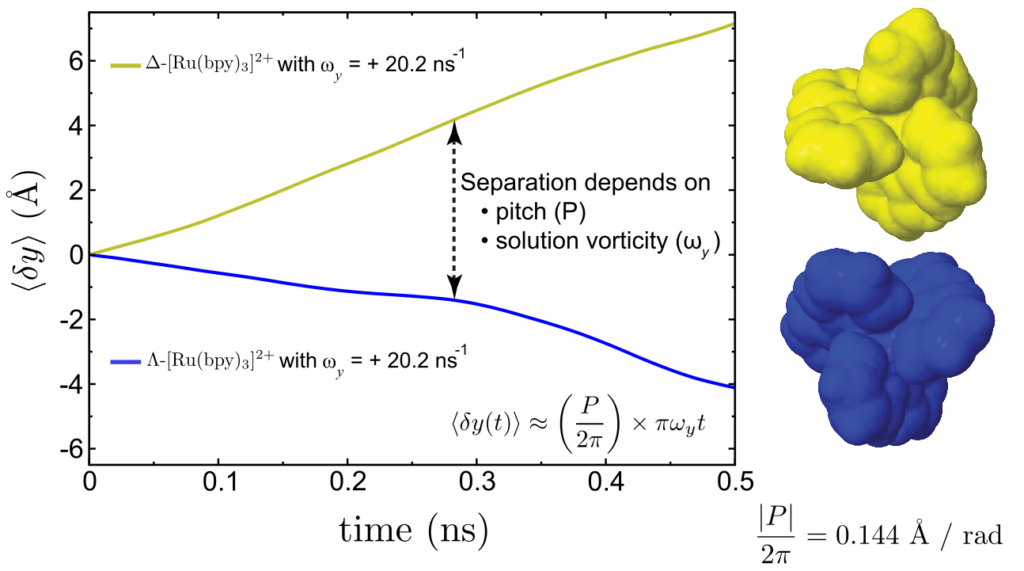
In this project, we discovered that this geometric property (the pitch of a screw) can be extended to molecules. Enantiomers have molecular pitch values with the same magnitude, but with flipped signs, moving in opposing directions under the same rotation source. As a consequence, this enables the separation of enantiomers.

**Figure 2**: Molecular pitch is a direct analogy to the pitch of screws. A typical wood screw might have a pitch measured in millimeter (mm) per radian of rotation, while molecules have a pitch in the order of 0.1 angstrom (Å) per radian of rotation.

Computer Science

Significant algorithmic development has gone into both the numerical calculation of molecular pitches and molecular dynamics simulations of solvated enantiomers to verify our predictions. The computed molecular pitches match the molecular dynamics simulations and can be estimated on a time scale of seconds, while the simulations require days or weeks of computer time.

Python code to compute the molecular pitches accompanies the publication and a C++ version of the same code is available as a program in OpenMD. The molecular dynamics simulations were carried out using OpenMD.

Common Name	Generic Name	CAS Number	Molecular Pitch \| P \| / 2π (in Å /rad)
Aricept	Donepezil	120014-06-4	0.267
Casodex	Bicalutamide	90357-06-5	0.246
Lipitor	Atorvastatin	134523-00-5	0.125
Nexium	Esomeprazole	119141-88-7	0.145
Paxil	Paroxetine	61869-08-7	0.159
Singulair	Montelukast	158966-92-8	0.325
Zoloft	Sertraline	79617-96-2	0.110
(Λ or Δ)-[Ru(bpy)₃]²⁺		50525-27-4	0.144
(S)-(−)-1,1′-binaphthyl-2,2′-diamine		18531-95-8	0.222
CHBrClF		593-98-6	0.0129

Table 1: Molecular pitches for some common enantiomeric molecules. Pitch data on 78 additional molecules are provided in Table S2 of the Supporting Information.

**Figure 3**: Under the same rotation \(\omega_y =\) 20.2 ns^-1, isolated Λ-[Ru(bpy)₃]²⁺ and Δ-[Ru(bpy)₃]²⁺ enantiomers move in opposite directions from their initial positions. The approximate mean displacement \(\langle \delta y(t) \rangle\) can be estimated from solution vorticity and the molecular pitch.

Engineering

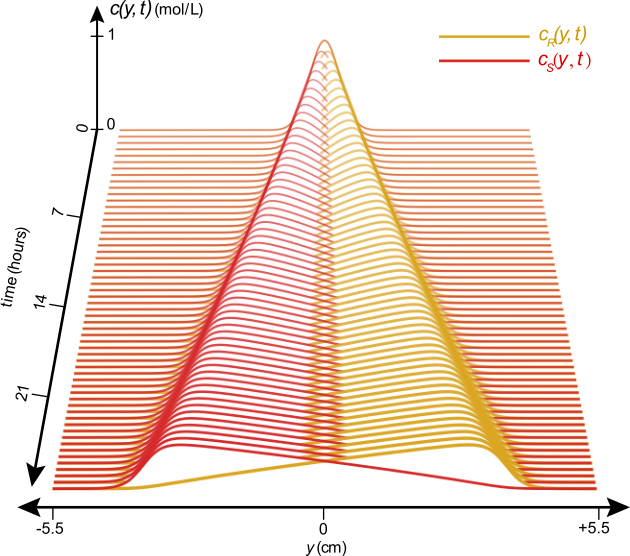
This work also allowed us to suggest design parameters for a device to separate enantiomers on a centimeter length scale using shear flow. This separation can be achieved in hours, when theoretically injecting a 1:1 mixture of enantiomers whose molecular pitch is 0.1 Å / rad in a machine that provides a constant vorticity of 10⁶ s^-1. Figure 4 below shows the estimated separation of the concentration profiles as a function of time in a hypothetical Taylor-Couette device.

**Figure 4**: Enantiomeric separation of a 1:1 mixture (racemic mixture). The mixture of R (yellow) and S (red) with a Gaussian concentration profile is injected at \(y=0 \) and \(t=0 \). The two enantiomers (R and S) separate on a centimeter length scale in a few hours. Each successive concentration curve c(y,t) is 30 minutes later than the curve above.

Other Applications

“Think of the Possibilities!”

Because our work relies on a first-principle approach, i.e., without data fitting, we can apply the same theory to large objects. For example, we can predict very similar behavior to the experiments on ferromagnetic microparticle ‘swimmers’ that were recently propelled through a stationary fluid using magnetic rotation by Cheang et al.

(Part of the “swimming_far_from_boundary.avi” video in Suplemental Material of Cheang et al.’s paper)

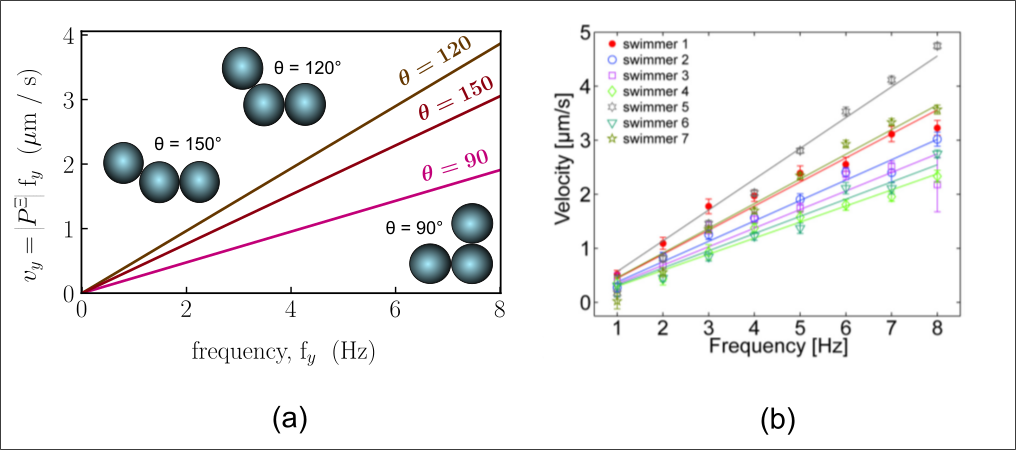
**Figure 5**: Velocity vs rotation frequency of the microparticle ‘swimmers’ from (a) this work (theory) and (b) experimental data obtained by Cheang et al. (FIG. 3. (b) from their paper).

As a final remark, the theory behind this work can be applied to objects of any scale and has the potential to reduce the cost of drug molecules, which are commonly pure enantiomers which currently do not have a general method of separation.