By Suzie Neidhart
When small particles of gold (a few nanometers in diameter) are exposed to light in the near-infrared portion of the spectrum, they absorb a significant amount of energy. This absorption of energy, and the way this energy dissipates into the surrounding environment, can be used to diagnose and treat certain forms of cancer. What we want to understand is how the morphology (shape) of these nanoparticles, and the chemical identity of the protecting layer that is bonded to the surface of the particles, can change the way the energy dissipates into the surroundings.
How does heat move?
On a microscopic level, heat is conducted through different mechanisms depending on the composition of the system. In a gas, heat is transferred primarily through collisions, while in semiconductors, thermal energy moves through the propagation of vibrations in the solid, or phonons. A phonon is a wave that traverses the material. Phonons can have both longitudinal or transverse polarization \((p)\). In metals, where the material has a solid lattice and a sea of electrons, both phonons and electronic heat conduction must be considered, and the electrons in a metal are typically treated as an electron gas. Electrons travel at velocities that are approximately three orders of magnitude faster than phonons, so the electronic contribution dominates heat transfer, and must be taken into account when considering bulk thermal conductivity of metals. However, at the interface between a metal and a non-metal, the thermal conductance into the non-metal is dominated by phonon scattering at the interface, rather than electronic contributions.
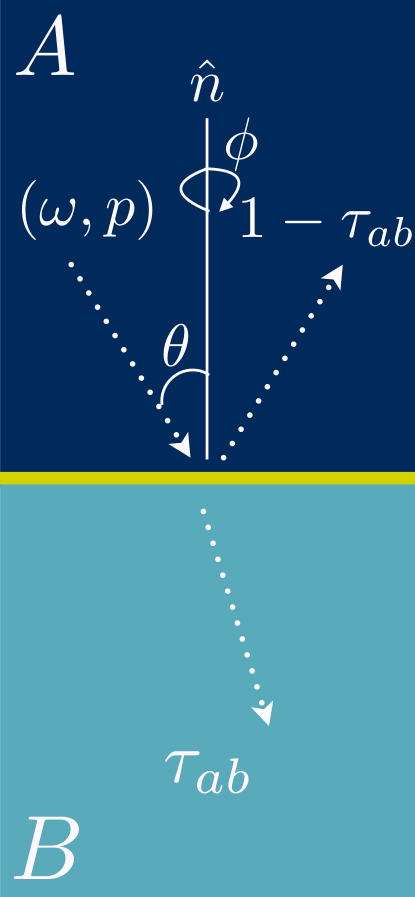
Phonon motion can be described relative to the interface between materials. An incoming phonon in material A approaches the interface between materials A and B. The wave has a polarization \((p)\) and frequency \((\omega)\) and approaches the interface with angles \(\phi\) and \(\theta\) relative to the normal to the interface. This phonon has a transmission probability, \(\tau_{\left\{\mathrm{A}\rightarrow\mathrm{B}\right\}}\left(p, \omega, \theta, \phi\right)\), that the wave will continue into material B (and carry with it a small amount of heat). We can make a few assumptions about how phonons scatter at the interface, and these assumptions yield both the widely-used acoustic mismatch model (AMM) and diffuse mismatch model (DMM).
Under the DMM, the phonon has only two options at the interface: it can scatter through the interface to material B or scatter back into material A. The probability of transmission is given by \(\tau_{\left\{\mathrm{A}\rightarrow\mathrm{B}\right\}}\left(\omega\right)\). Due to the fact the DMM must obey detailed balance, the scatter back to material A is \(\tau_{\left\{\mathrm{A}\rightarrow\mathrm{A}\right\}}\left(\omega\right) = 1 – \tau_{\left\{\mathrm{A}\rightarrow\mathrm{B}\right\}}\left(\omega\right)\).
Thermal Transport at Interfaces
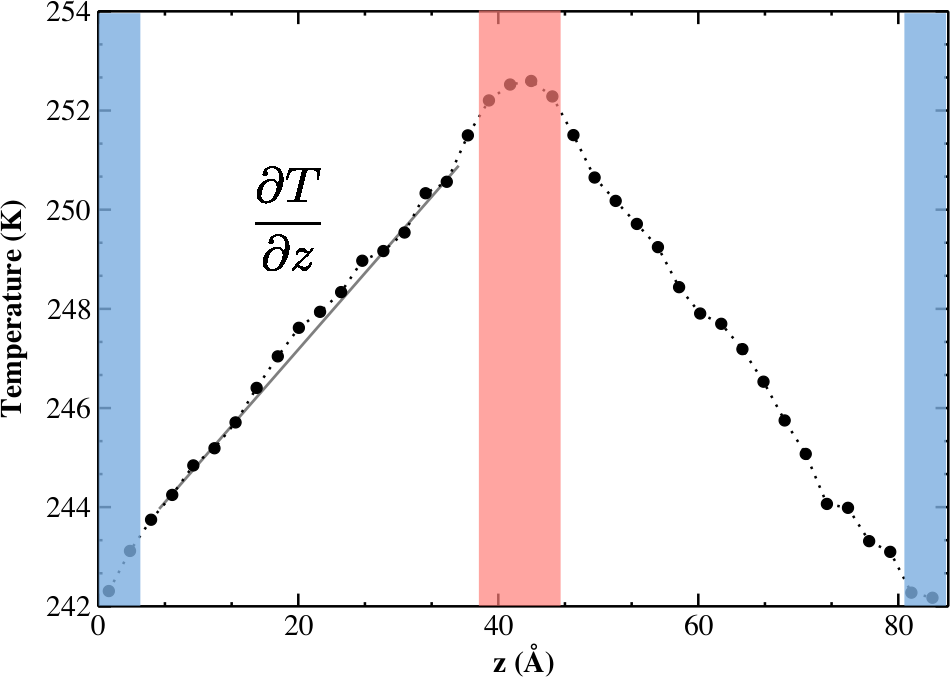
We model heat transport in real molecular systems using a computational method that creates steady-state non-equilibrium conditions in our simulations. Reverse Non-Equilibruim Molecular Dynamics (RNEMD), uses a series of velocity scaling transformations for the atoms in material A and material B. This imposes a thermal flux \((J_z)\) in planar systems, or a heat rate \((q_r)\) in spherical geometries. The system responds to the imposed flux by developing a temperature gradient \(\left(\partial T / \partial z \right)\) in bulk regions and a temperature discontinuity \(\left(\Delta T\right)\) at an interface. The temperature profile can therefore tell us about the thermal conductivity of a bulk material, or at an interface, the interfacial thermal conductance \((G)\).
\(\begin{align} J_z & = G \Delta T \\ J_r &= \frac{q_r}{A} = G \Delta T\end{align}\)For planar interfaces between gold films and a solvent, the interfacial thermal conductance \((G)\), can be found by measuring the temperature difference between the outer-most gold layer and the inner-most solvent layer. For nanoparticles, the details of how the temperature changes between the outer-most gold layer and the inner-most solvent layer are important. We calculate the thermal boundary resistance as a series of thermal resistors that include any chemicals bound to the surface of the particles.
Morphology (Shape) Dependence
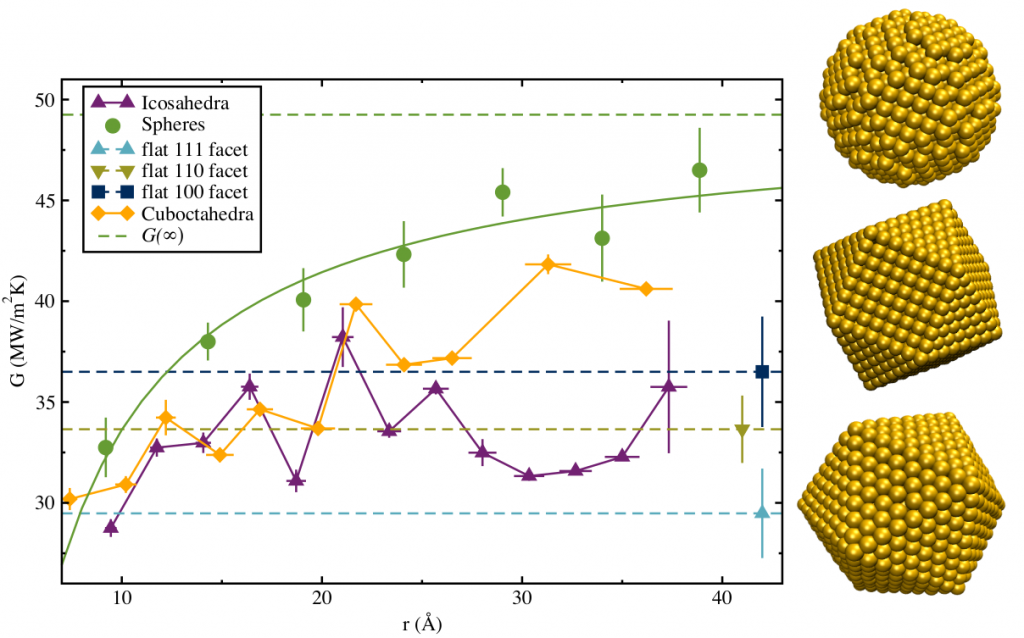
Starting with a simple system of bare gold particles and a non-polar solvent, three nanoparticle morphologies were investigated: spheres, icosahedra, and cuboctahedra. These three particles display different facets of gold to the surrounding solvent. Also, because we are studying a non-polar solvent, we do not take into account electronic contributions to thermal conductivity.
Our simulations of particles from 8-42 Å in radius, and additional simulations of the individual flat facets of gold, show fascinating trends. Specifically, that the interfacial thermal conductance depends largely on the fractional surface area occupied by each facet.
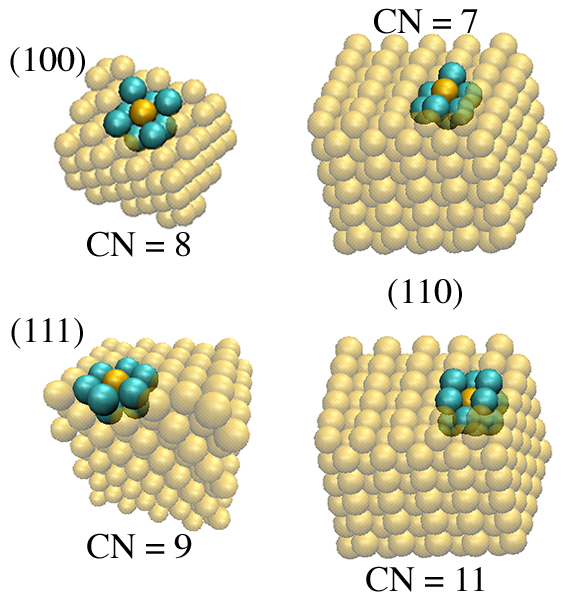
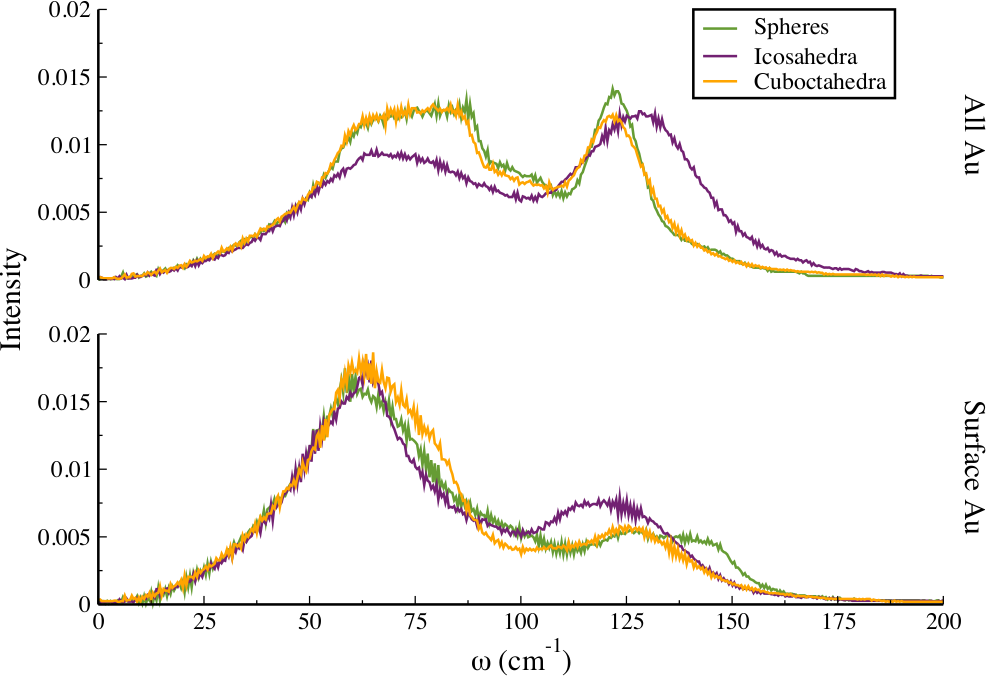
This idea can be further explored by examining the coordination number (how many neighbors each surface atoms has) for the surfaces of the different particles and planar systems. Coordination information and a vibrational density of states for the different coordination environments elucidates the vibrational freedom that is given to the heat carriers at the surface. Here the vibrational power spectrum is used to approximate the density of states used in the DMM and the AMM.
In addition to the surface vibrational density of states, the total vibrational density of states of the nanoparticle structures can show which phonon modes are occupied in different structures and sizes. We showed that spheres and cuboctahedra (both ‘FCC’ structures) have the same low frequency spectra, while the icosahedra have different packing, and a significantly different vibrational density of states.
Ligand Dependence
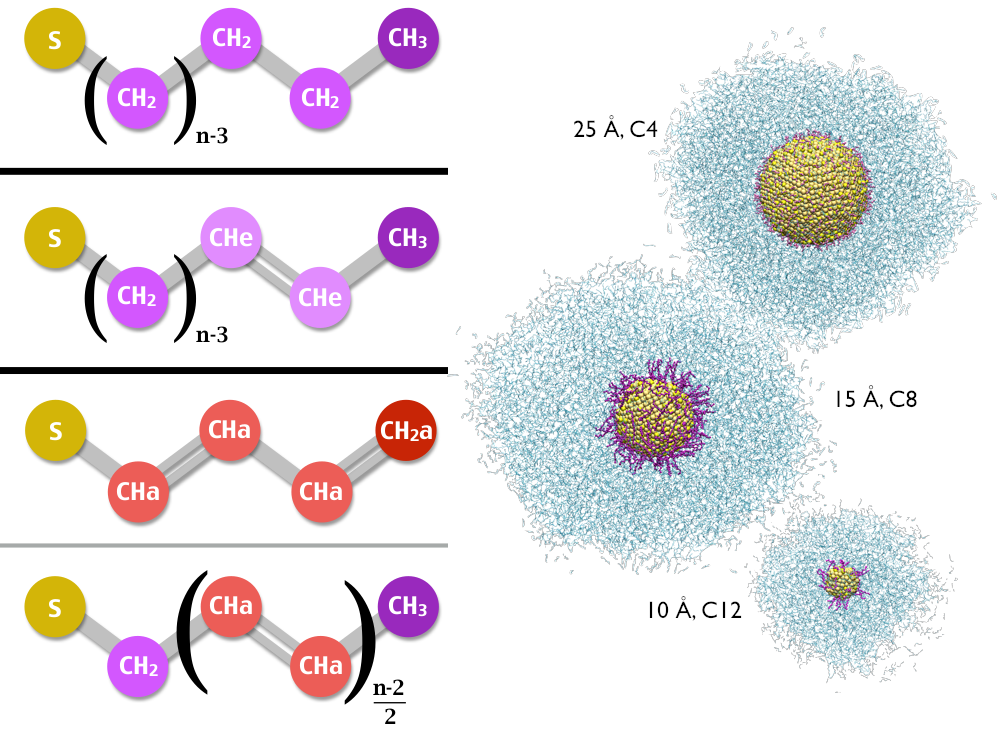
To investigate the role of the protecting layer of molecules bound to the surface of the nanoparticles, we also used these same spheres as a ‘core’ and then attached thiolate ligands as a protecting layer on the surface. We used non-polar solvents and non-polar ligands to investigate the effect of ligand length and ligand rigidity. The ligands were packed at 50% coverage of the surface on a set of 4 different sizes of particles.
The surface features all play a small role in thermal conductance at the interface. These include:
- ligand ordering at the surface,
- the density of material at the interface and beyond, and
- the physical overlap of the ligand and the solvent (measured via interpenetration of the solvent to the ligand layer)
In addition to the physical behavior of the interface layer, the vibrational density of states shows us which phonon modes overlap and allow better transmission from one material to another. We find that the overlap in both the vibrational density of states and the physical density are essential to optimize heat transfer.
Nanoarrays
Bulk thermal conductivity simulations have been used to study systems containing solvated nanoparticle arrays. In particular, we have simulated nanoarrays of Au144PET60, a small nanocluster with a liquid gold core and staple-motif ligands on the surface. These particles are then solvated in toluene (and separately with dichloromethane) and packed in a simple cubic structure, although they are free to diffuse away from their initial positions.

A predictive model for the thermal conductivity of composite materials was proposed in 1987 by Hasselman and Johnson using bulk material properties like the bulk thermal conductivity of the solvent \((\lambda_s)\) and the volume fraction of the particles \((v_p)\). Because bulk materials exhibit thermal conductivity that depends on simulation box length; the conductivities for both solvents and the gold were projected to an infinite box length.
Our predictions of the composite material thermal conductivity depend primarily on the volume fraction of the particles but are much higher than current simulation results for relatively small \((2 \times 2 \times 2)\) nanoarrays. Simulations that will project to infinite box sizes are ongoing.
