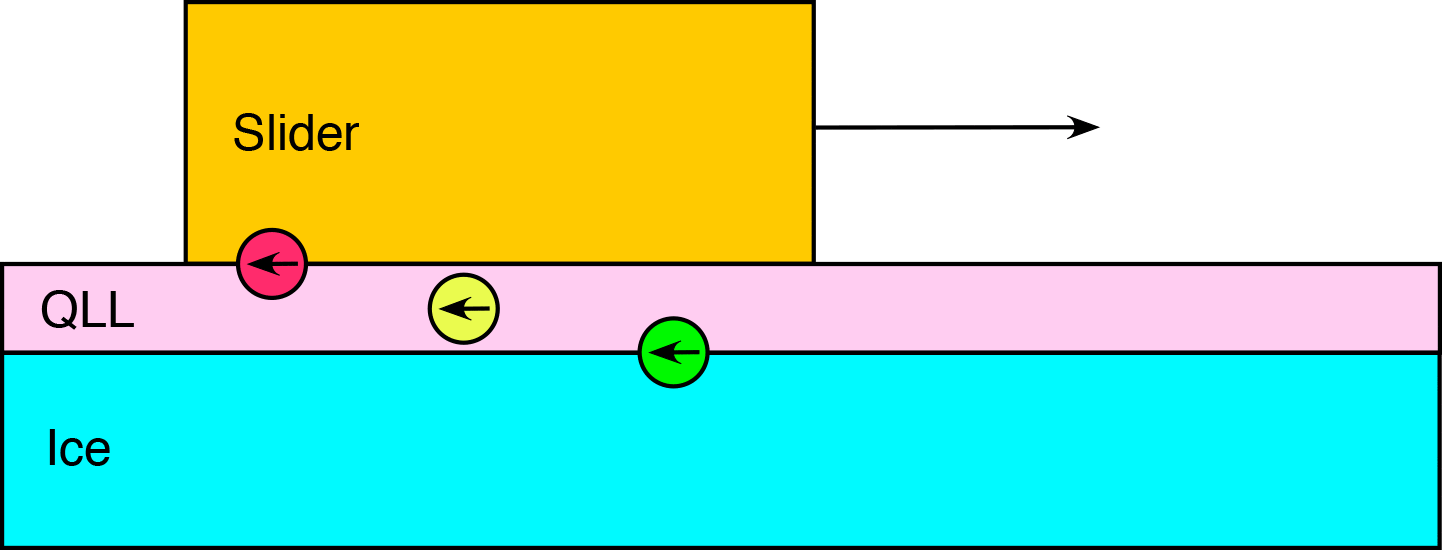
Hydrodynamic Friction

There are three general contributions to hydrodynamic friction at ice surfaces. The ice-to-QLL solid/liquid friction (green), the viscous shearing of the QLL (yellow), and the capillary bridges formed between the QLL and the slider (red). Friction at the ice/QLL interface has recently been observed to be dependent on the exposed crystal facet. The width of this interface has been estimated, and the structure and dynamics of water molecules in this region have been characterized. From this, a simple momentum transmission model has been proposed which accurately captures the molecular origins of the observed ice/QLL friction. A spatially resolved estimate for the shear viscosity of the QLL has also been estimated. Close to the ice surface, the shear viscosity of the QLL is close to that of chocolate syrup (~10,000 cP), while closer to the vapor interface the viscosity is much smaller, (1-10 cP).

Crystal Facets of ice-Ih

Under ambient conditions water crystallizes into ice-Ih, which commonly forms hexagonal plates. The basal face forms the top and bottom of these plates, and the sides of these plates expose the prismatic facet. Other less-common but still important faces are the pyramidal and secondary prismatic. Side-on views of these faces are shown to the right, with the surface oxygen atoms colored in blue.

Shearing at Ice / Water Interfaces

Using our Velocity Shearing and Scaling variant of Reverse Non-Equilibrium Molecular Dynamics (VSS-RNEMD), solvated ice crystals were drawn through liquid water. The temperature at the interface was maintained at the coexistence temperature by a weak thermal gradient (below).

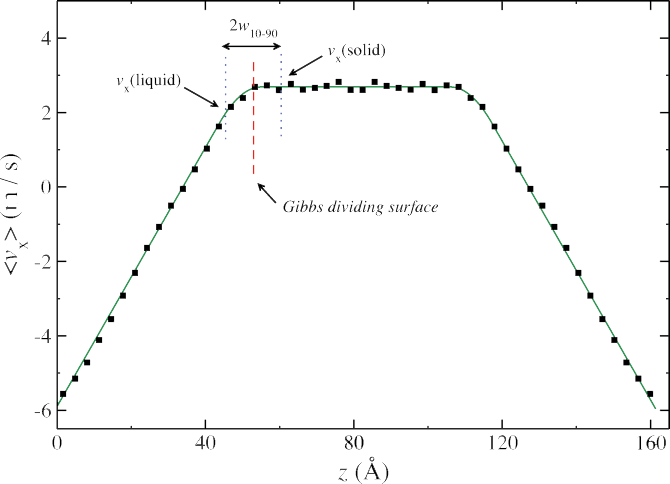
Interfacial Momentum Conductance

The interfacial momentum conductance (kappa) is easily computed as a ratio of the imposed momentum flux to the velocity drop across the ice / water interface (right). However, defining the width of this interface is somewhat subjective to the choice of order parameter. We have estimated the interfacial width using structural and dynamic order parameters, and in general find that structural measures of the interface are slightly smaller (7 – 9 Å) than dynamic measures (10 – 15 Å).

Interestingly, we have observed isotropic interfacial momentum conductance for shearing relative to the orientation of the surface features shown above.

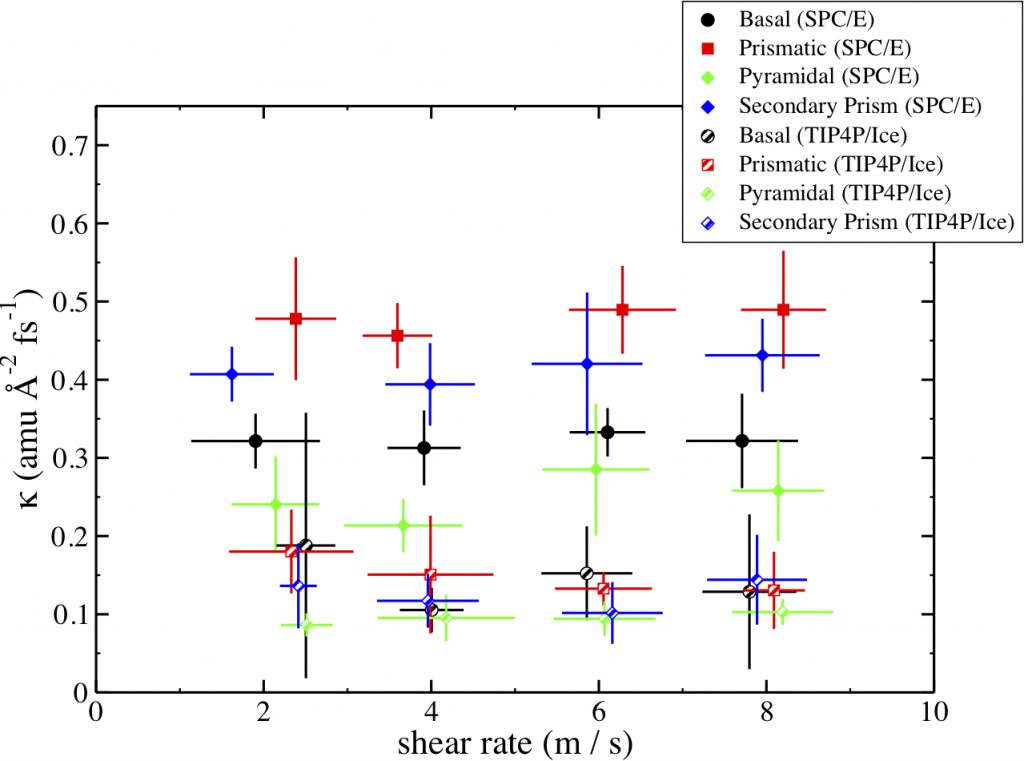
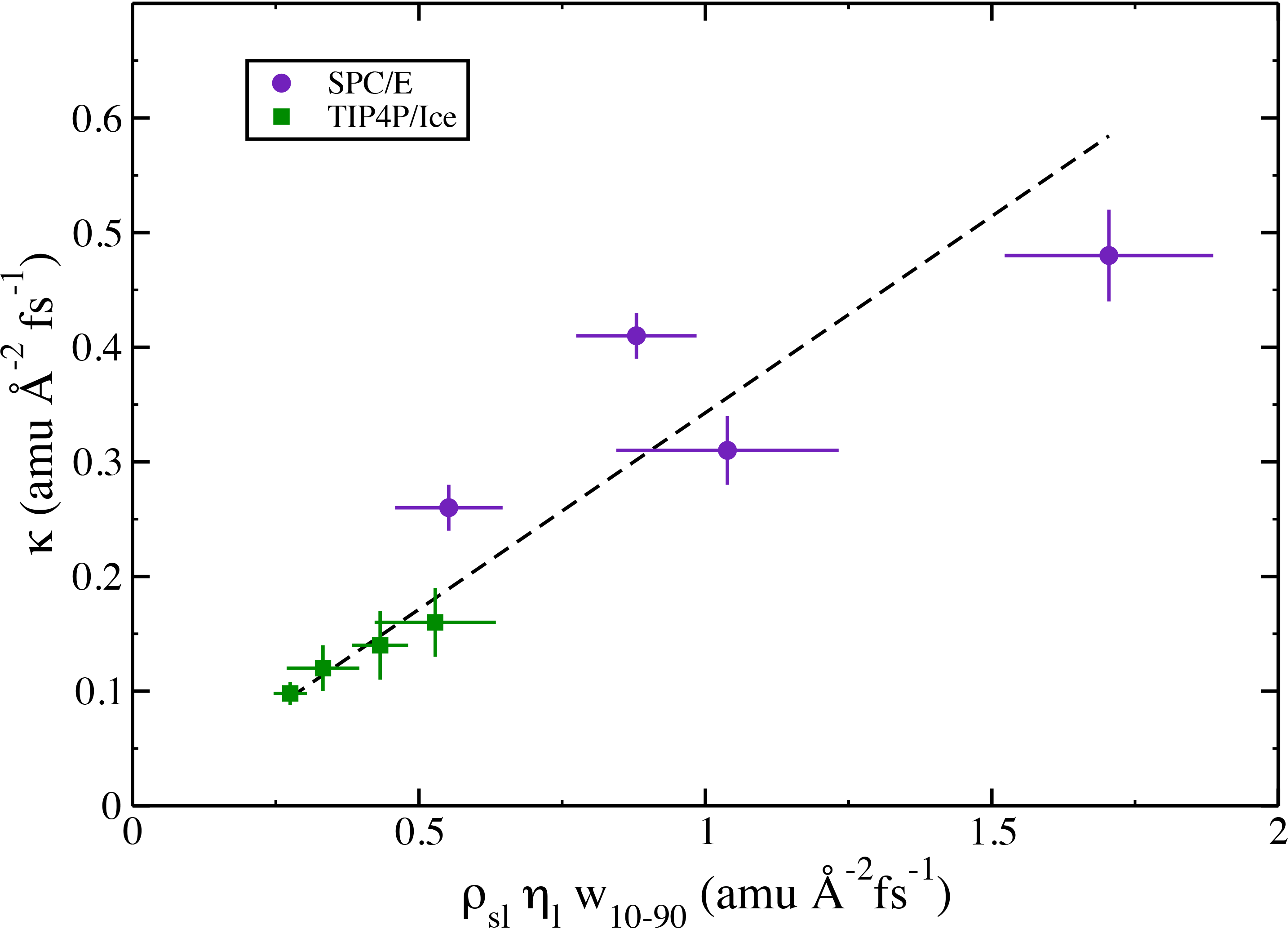
Left: The interfacial momentum conductance for the four crystal faces using both the SPC/E and TIP4P/Ice water models. We see kappa is larger for the SPC/E modeled systems as compared with the TIP4P/Ice systems. However, we see that the same ordering of kappa values is observed by both models. The prismatic facet displays the largest momentum conductance, the secondary prismatic is slightly smaller, the basal displays moderate momentum conductance, and the pyramidal has the smallest.

Density Projections of Ice / Water Interfaces

Density projections were computed to investigate the effect of the surface corrugation of the ice crystals. The prismatic and secondary prismatic surfaces present well defined channels to the liquid. In contrast, the basal surface is relatively flat. The pyramidal face displays much wider channels that are shallower than the two prismatic channels.

Querying these density plots, we have obtained estimates of the surface channel dimensions. In addition, we have found that the channels are very robust under shear, no interfacial liquid molecules we found within the channels. Interestingly, we see templating of the liquid by the presented ice surface beyond the Gibbs dividing surface as determined by the local tetrahedral order parameter.

Hydrogen-Bond Density at the Ice / Water Interface

An ice facet which forms more hydrogen-bonds with the liquid would impose a larger drag on the fluid flowing past the surface. Commonly, hydrogen-bonds are identified based on a geometric or energetic criteria. Since the energies of water clusters are highly dependent on their geometries, the two definitions are intimately coupled. The hydrogen bond donor (D) and acceptor (A) ice, interfacial, and liquid water molecules were identified by their local tetrahedral order parameter value (q).

Heat maps of the relative populations of hydrogen-bonds between donor and acceptor molecules tabulated by q can be used to determine the density of solid-to-liquid hydrogen bonds at each of the interfaces. Since there is no clear division between q of pure ice and q of pure liquid (top), a cutoff of value must be established. We have chosen our cutoff as the value at the Gibbs dividing surface between the solid and the liquid, q=0.84. We see a positive correlation between the momentum conductance with the density of solid-to-liquid hydrogen bonds normalized by the presented surface area.

Momentum Transmission Model

The momentum should be conducted across the interface through strong intermolecular forces (hydrogen-bonds). Therefore, the momentum conductance should be described by a simple transmission model. We have found agreement with a model which incorporates the amount of these strong intermolecular interactions, the shear viscosity of the liquid (eta) which describes the movement of the momentum away from the interface, over an interface of some width (w).

The estimates obtained by the TIP4P/Ice model agree very well with this simple model, while estimates by the SPC/E model are scattered around the line of best-fit. Since the TIP4P/Ice model was parameterized to reproduce the melting temperature of ice correctly, it is encouraging that the transmission model agrees strongly with these results.

The Quasi-Liquid Layer of Ice

At temperatures approaching the melting point, all solids exhibit a surface premelting due to the truncation of the crystal lattice. For water ice, the onset of the this surface premelt has been observed at temperatures between 180 K to 260 K, depending on the method for probing the surface molecules. Techniques which rely on a large collection of molecules indicate a warmer onset temperature, while single molecule techniques indicate a lower temperature. Computer simulations of vacuum exposed ice also predict this phenomenon. Below, the vacuum exposed basal crystal face modeled using TIP4P/Ice at 10 K of undercooling.

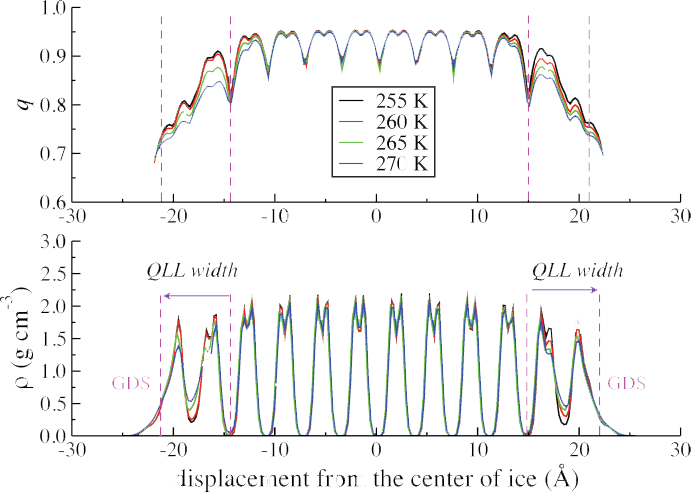
The vacuum exposed basal face of an ice-Ih crystal at temperatures of 0 K to 15 K of undercooling exhibits the formation of a quasi-liquid layer apparent in both the transverse density and local tetrahedral order parameter. We define the start of the QLL to be the location of the last un-wetted crystal surface, and truncate the QLL at the distance from the ice crystal where the density goes to 0.5 g/cm^3.

Diffusion of Water in the QLL

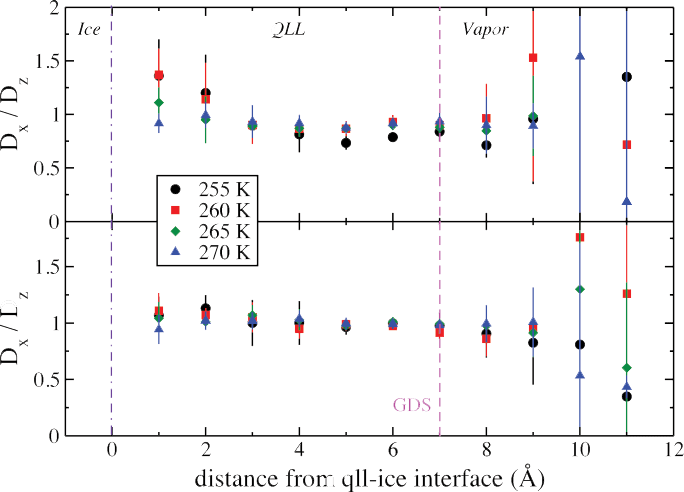
One-dimensional diffusion constants were computed for molecules in small bins normal to the interface. The basal face displays isotropic diffusion, although it has been predicted that for extremely thin QLLs the surface, which displays six-fold symmetry, may exhibit anisotropic diffusion. In contrast, we observe anisotropic diffusion at the prismatic surface at these warmer temperatures.

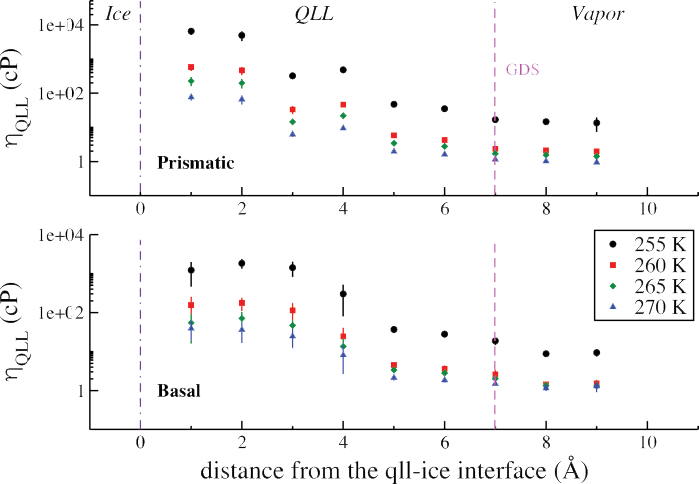
Shear Viscosity of the Quasi-Liquid Layer

We have computed spatially resolved estimates of the shear viscosity of the quasi-liquid layer at the basal and prismatic faces of an ice-Ih crystal. We see a drastic change in the viscosity close to the surface of ice compared to near the vapor interface. Near the ice, we find shear viscosity of the QLL on the prismatic surface (10,000 cP) is larger than found on the basal surface (1,000 cP). This agrees well with the larger momentum conductance measurements reported above.

At the vapor interface, we observe estimates of the shear viscosity around 1-10 cP. We attribute the low friction observed on ice to be due to the small shear viscosity at the vapor interface.